Title Generator
The point of this post is pretty straightforward: apply an encoder-decoder Transformer model to yet another text generation task. The problem at hand is to generate a title given the abstract of a scientific paper.
I’m trying to figure out how to have Jupyter notebooks on WordPress; the export to HTML seems fine, but it’s hard to run. This notebook can be downloaded from here.
Load and process data
We will use the Arxiv dataset which consists of 1.7 million articles with parsed information. The dataset is quite large at over 3GB, and we’ll be only interested in using a small subset. Thus, we first process this by only parsing out a set number of articles’ title and abstract which are from a specific scientific field.
We use read_json from pandas to process the data file, remove all other columns and create a single DataFrame after removing leading/trailing white space and newline characters.
# Pytorch
import torch
from torch.utils.data import Dataset, DataLoader, random_split
from torch.nn.utils.rnn import pad_sequence
from torch import nn
import torch.optim as optim
import pandas as pd
from tqdm.notebook import tqdm
from matplotlib import pyplot as plt
import math
import numpy as np
# Let's set some variables for the data processing part
TOTAL_ARTICLES = 300000
FIELD = 'astro'
# We read a few lines at a time; note that if `chunksize` is none, the whole thing is read to memory
chunks = pd.read_json('arxiv-metadata-oai-snapshot.json', lines=True, chunksize=2048)
astro_dfs = []
num_articles = 0
for entries in tqdm(chunks):
# We find all articles of a certain field, and then discard the rest of the columns
astro_dfs.append(
entries[entries['categories'].str.contains(FIELD)].drop(
['id', 'submitter', 'authors', 'comments', 'journal-ref', 'doi',
'report-no', 'categories', 'license', 'versions',
'update_date', 'authors_parsed'], axis='columns'
)
)
num_articles += len(astro_dfs[-1])
# We stop once we have enough of a dataset
if num_articles > TOTAL_ARTICLES:
break
# Make one dataframe, and we remove the \n in the text
data_df = pd.concat(astro_dfs, ignore_index=True)
data_df = data_df.replace(r'\n',' ', regex=True)
data_df['title'] = data_df['title'].str.strip()
data_df['abstract'] = data_df['abstract'].str.strip()
data_df
Tokenize Data
With the text in an easy to manipulate DataFrame, we have to convert the text to a numerical representation. Here, we use pre-trained tokenizers from Huggingface rather than build/train our own. Roughly speaking, a tokenizer takes a word and maps it to an integer. However, often times, modern tokenizers “understand” parts of words and would also parse out the prefix/suffix of a word too.
For simplicity, we’re only going to use 384 tokens for the abstract and 64 tokens for the title, and discard the rest. This is usually not a problem for the title (as it is quite short), but will generally truncate the abstract. However, judging from the box plot, the number of tokens seem fine. Ideally, our model would incorporate the full abstract, however the amount of compute power needed will be a lot larger due to the quadratic scaling of the transformers.
from transformers import AutoTokenizer
checkpoint = "bert-base-uncased"
tokenizer = AutoTokenizer.from_pretrained(checkpoint)
# This is fairly slow,
data_tokenized = pd.DataFrame()
data_tokenized['abstract'] = data_df['abstract'].apply(
lambda w: torch.Tensor(tokenizer(w, truncation=True, max_length=256+128)['input_ids']).int()
)
data_tokenized['title'] = data_df['title'].apply(
lambda w: torch.Tensor(tokenizer(w, truncation=True, max_length=64)['input_ids']).int()
)
plt.boxplot(data_tokenized['abstract'].str.len(), vert=False)
plt.boxplot(data_tokenized['title'].str.len(), vert=False)
plt.show()
Data Loader
With the data in a numerical form, we can start loading them into PyTorch Dataset/DataLoader objects. This will help facilitate easier training.
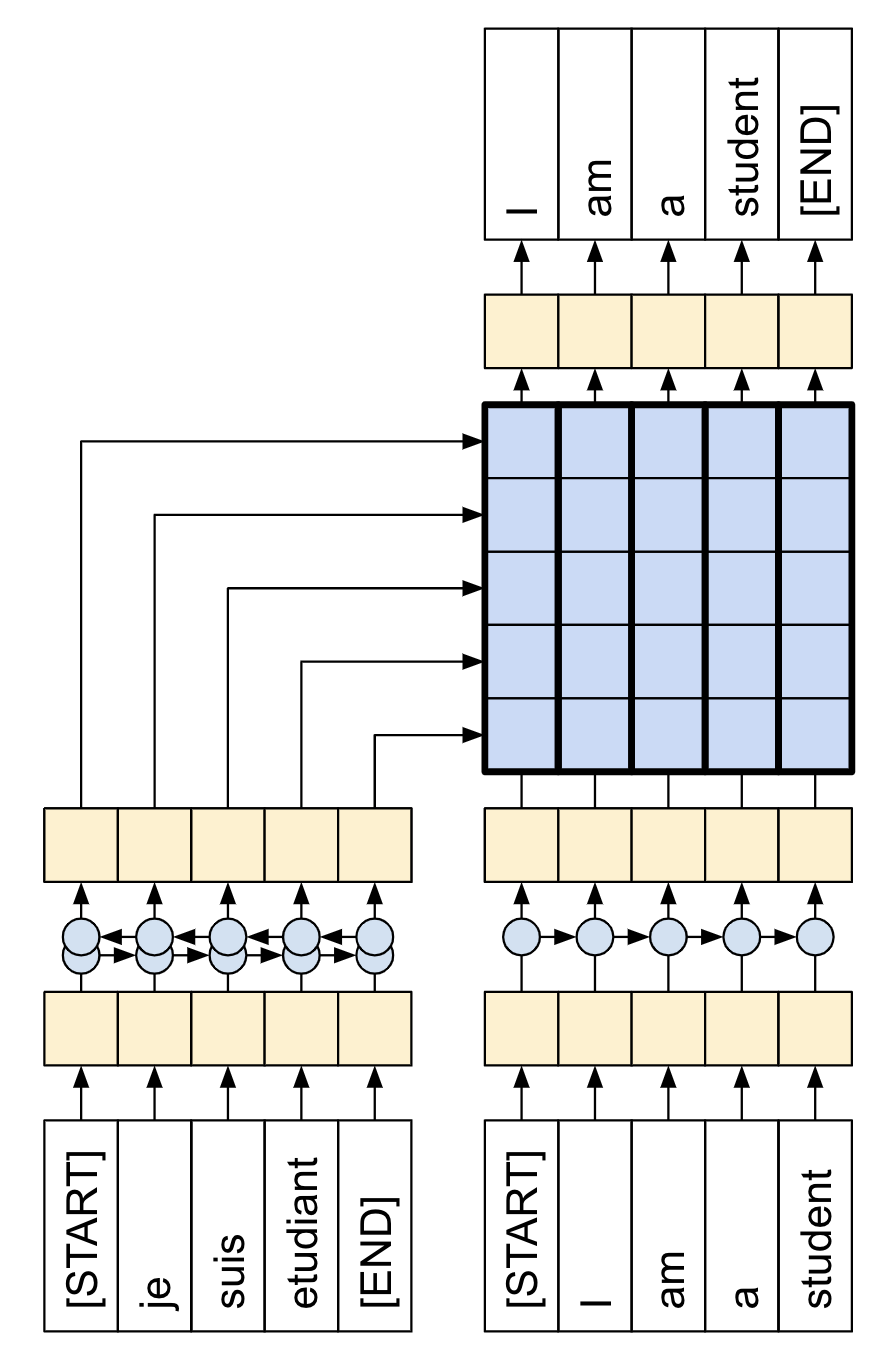
Here, we note that we want to generate datasets which are applicable for “teacher forcing” learning. In our case, we want to deduce a sequence $(x_1, x_2, \ldots, x_{n+1})$ from $(x_0, \ldots, x_n)$. See figure (source) below. In our case the French corresponds to the abstract while the English is the title. This means that we would need to shift the titles by 1 in the collate_fn function for the DataLoader. We also take the opportunity here to perform the train/validation split.

class ArxivDataset(Dataset):
def __init__(self, dataframe):
self.df = dataframe
def __len__(self):
return len(self.df)
def __getitem__(self, idx):
"""
Returns abstract, then title
"""
return self.df.iloc[idx, 0], self.df.iloc[idx, 1]
def pad_collate(batch):
my_abstracts, my_titles = zip(*batch)
# Pad sequence together, with 0 added
my_abstracts = pad_sequence(my_abstracts, batch_first=True)
my_titles = pad_sequence(my_titles, batch_first=True)
# For teacher training, need to shift
titles_inp = my_titles[:, 0:-1]
titles_lab = my_titles[:, 1:]
return (my_abstracts, titles_inp), titles_lab
dataset = ArxivDataset(data_tokenized)
train_size = int(0.8 * len(dataset))
test_size = len(dataset) - train_size
train_dataset, test_dataset = random_split(dataset, [train_size, test_size])
train_dataloader = DataLoader(train_dataset, batch_size=256+64, shuffle=True, collate_fn=pad_collate)
test_dataloader = DataLoader(test_dataset, batch_size=256+64, shuffle=True, collate_fn=pad_collate)
print(len(train_dataloader), len(test_dataloader))
Transformer model
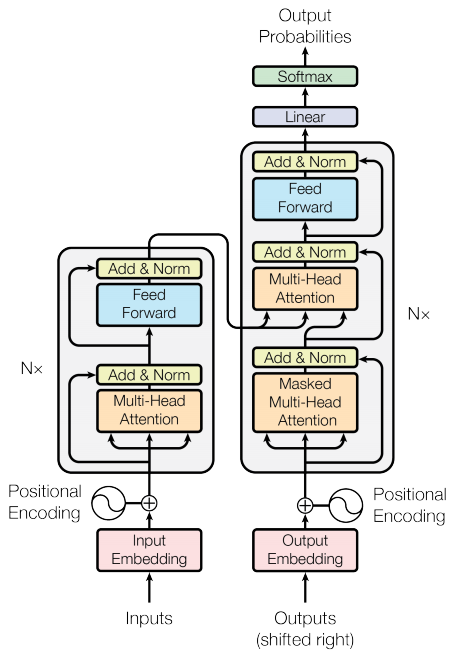
Note that this is not intended as a tutorial for how to build a transformer, and we will gloss over most details. Roughly speaking, a transformer is a sequence-to-sequence model which supplies the probability distribution of the next element. First the abstract is embedded in some latent space by the encoder, which is then use by the decoder to condition for the prediction.
It is similar to RNNs, however, the main technique for a transformer is the attention mechanism, which is implemented in PyTorch. This allows transformers, in theory, to couple far ranging words with each other rather easily as a quadratic 1-to-1 comparison is done between every element in the sequence. With this extra $n^2$ expense, comes at a benefit of it seemingly able to learn languages very well.
PyTorch in theory has a Transformer module but it is not well documented. We will perform a quick and dirty implementation here. For more details, we refer to a great tutorial here. The schematics below should serve as enough of a guideline for the code below.
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
Positional Embedding
class PositionalEncoding(nn.Module):
def __init__(self, d_model, max_len=5000):
"""
Inputs
d_model - Hidden dimensionality of the input.
max_len - Maximum length of a sequence to expect.
"""
super().__init__()
# Create matrix of [SeqLen, HiddenDim] representing the positional encoding for max_len inputs
pe = torch.zeros(max_len, d_model)
position = torch.arange(0, max_len, dtype=torch.float).unsqueeze(1)
div_term = torch.exp(torch.arange(0, d_model, 2).float() * (-math.log(10000.0) / d_model))
pe[:, 0::2] = torch.sin(position * div_term)
pe[:, 1::2] = torch.cos(position * div_term)
pe = pe.unsqueeze(0)
# register_buffer => Tensor which is not a parameter, but should be part of the modules state.
# Used for tensors that need to be on the same device as the module.
# persistent=False tells PyTorch to not add the buffer to the state dict (e.g. when we save the model)
self.register_buffer('pe', pe, persistent=False)
def forward(self, x):
x = x + self.pe[:, :x.size(1)]
return x
Encoder Block
This just consists of a multihead attention (essentially a few attentions concat-ed together), and a feed-forward NN.
class EncoderBlock(nn.Module):
def __init__(self, input_dim, num_heads, dim_feedforward, dropout=0.1):
super().__init__()
# Attention layer
self.self_attn = nn.MultiheadAttention(
embed_dim=input_dim,
num_heads=num_heads, batch_first=True
)
# Two-layer MLP
self.linear_net = nn.Sequential(
nn.Linear(input_dim, dim_feedforward),
nn.Dropout(dropout),
nn.ReLU(inplace=True),
nn.Linear(dim_feedforward, input_dim)
)
# Layers to apply in between the main layers
self.norm1 = nn.LayerNorm(input_dim)
self.norm2 = nn.LayerNorm(input_dim)
self.dropout = nn.Dropout(dropout)
def forward(self, x):
# Attention part
attn_out, _ = self.self_attn(x, x, x)
x = x + attn_out
x = self.norm1(x)
# MLP part
linear_out = self.linear_net(x)
x = x + self.dropout(linear_out)
x = self.norm2(x)
return x
class EncoderLayers(nn.Module):
def __init__(self, num_layers, **encoder_args):
super().__init__()
self.layers = nn.ModuleList([EncoderBlock(**encoder_args) for _ in range(num_layers)])
def forward(self, x):
for l in self.layers:
x = l(x)
return x
Decoder
A decoder layer consists of a causal attention, cross-attention from the decoder, and a final MLP.
# From PyTorch source
def _generate_square_subsequent_mask(
sz: int,
dtype: torch.dtype = torch.get_default_dtype(),
):
r"""Generate a square causal mask for the sequence. The masked positions are filled with float('-inf').
Unmasked positions are filled with float(0.0).
"""
return torch.triu(
torch.full((sz, sz), float('-inf'), dtype=dtype, device=device),
diagonal=1,
)
class DecoderBlock(nn.Module):
def __init__(self, input_dim, num_heads, dim_feedforward, dropout=0.1):
super().__init__()
# Attention layers
self.causal_self_attn = nn.MultiheadAttention(
embed_dim=input_dim,
num_heads=num_heads, dropout=dropout, batch_first=True
)
self.cross_attn = nn.MultiheadAttention(
embed_dim=input_dim,
num_heads=num_heads, dropout=dropout, batch_first=True,
)
# Two-layer MLP
self.linear_net = nn.Sequential(
nn.Linear(input_dim, dim_feedforward),
nn.Dropout(dropout),
nn.ReLU(inplace=True),
nn.Linear(dim_feedforward, input_dim)
)
# Layers to apply in between the main layers
self.norm1 = nn.LayerNorm(input_dim)
self.norm2 = nn.LayerNorm(input_dim)
self.norm3 = nn.LayerNorm(input_dim)
self.dropout = nn.Dropout(dropout)
def forward(self, x, context):
# Causal; create mask
mask = _generate_square_subsequent_mask(x.shape[1])
attn_out, _ = self.causal_self_attn(
x, x, x, attn_mask=mask, is_causal=True
)
x = x + attn_out
x = self.norm1(x)
# Cross attention
attn_out, _ = self.cross_attn(
x, context, context,
)
x = x + attn_out
x = self.norm2(x)
# MLP
linear_out = self.linear_net(x)
x = x + self.dropout(linear_out)
x = self.norm3(x)
return x
class DecoderLayers(nn.Module):
def __init__(self, num_layers, **decoder_args):
super().__init__()
self.layers = nn.ModuleList([DecoderBlock(**decoder_args) for _ in range(num_layers)])
def forward(self, title, abstract):
for l in self.layers:
title = l(x=title, context=abstract)
return title
Full Model
The transformer full model is simply the above two blocks, alongside some embeddings and a final classifier layer.
class Transformer(nn.Module):
def __init__(self, num_layers, model_dim, num_heads, dff,
vocab_size, dropout=0.2):
super().__init__()
# Needed for scaling
self.model_dim = model_dim
# Embedding
self.embedding = nn.Embedding(
num_embeddings=vocab_size, embedding_dim=model_dim
)
# Positional
self.positional_encoding = PositionalEncoding(d_model=model_dim)
self.encoder = EncoderLayers(
num_layers=num_layers, input_dim=model_dim, num_heads=num_heads, dim_feedforward=dff, dropout=dropout
)
self.decoder = DecoderLayers(
num_layers=num_layers, input_dim=model_dim, num_heads=num_heads, dim_feedforward=dff, dropout=dropout
)
# Final layer which maps to "probabilities" in the token space
self.ff = nn.Linear(model_dim, vocab_size)
def forward(self, title, abstract):
# Apply embedding and position
title = self.embedding(title) * math.sqrt(self.model_dim)
abstract = self.embedding(abstract) * math.sqrt(self.model_dim)
# Add positional
title = self.positional_encoding(title)
abstract = self.positional_encoding(abstract)
# Apply encoder than decoder
abstract = self.encoder(abstract)
title = self.decoder(title, abstract)
return self.ff(title)
Training
There are heuristics for training transformers; one of them is that a warmup should be used. We use the cosine warmup as detailed in the tutorial linked above. Another small caveat is that for the cross entropy loss, to ignore the index 0 (where padding occurred), as we don’t want the optimizer to optimize over dummy data.
Besides the two notes above, the below should be fairly similar to the usual training procedure.
class CosineWarmupScheduler(optim.lr_scheduler._LRScheduler):
def __init__(self, optimizer, warmup, max_iters):
self.warmup = warmup
self.max_num_iters = max_iters
super().__init__(optimizer)
def get_lr(self):
lr_factor = self.get_lr_factor(epoch=self.last_epoch)
return [base_lr * lr_factor for base_lr in self.base_lrs]
def get_lr_factor(self, epoch):
lr_factor = 0.5 * (1 + np.cos(np.pi * epoch / self.max_num_iters))
if epoch <= self.warmup:
lr_factor *= epoch * 1.0 / self.warmup
return lr_factor
def train(dataloader, my_model, my_criterion, my_optimizer, my_scheduler, my_epoch, interval=500):
"""
Training loop for one epoch
"""
losses = []
model.train()
for batch_idx, ((abstract, title_inp), title_lab) in enumerate(dataloader):
# Move to GPU
abstract = abstract.to(device)
title_inp = title_inp.to(device)
title_lab = title_lab.type(torch.long)
title_lab = title_lab.to(device)
pred = my_model(title_inp, abstract)
loss = my_criterion(
pred.reshape(-1, MAX_VOCAB), title_lab.reshape(-1)
)
my_optimizer.zero_grad()
loss.backward()
torch.nn.utils.clip_grad_norm_(my_model.parameters(), 5)
my_optimizer.step()
my_scheduler.step()
losses.append(loss.item())
if batch_idx print(f'Epoch {my_epoch} | {batch_idx / len(dataloader) * 100:.1f}return losses
def test(dataloader, my_model, my_criterion, my_epoch):
"""
Training loop for one epoch
"""
val_loss = 0
val_acc = 0
val_total = 0
model.eval()
with torch.no_grad():
for _, ((abstract, title_inp), title_lab) in enumerate(dataloader):
# Move to GPU
abstract = abstract.to(device)
title_inp = title_inp.to(device)
title_lab = title_lab.type(torch.long)
title_lab = title_lab.to(device)
title_lab = title_lab.reshape(-1)
pred = my_model(title_inp, abstract)
pred = pred.reshape(-1, MAX_VOCAB)
loss = my_criterion(
pred, title_lab
)
val_loss += loss.item()
# Count number of correct predictions
pred = torch.argmax(pred, dim=1, keepdim=True)
title_lab = title_lab.reshape_as(pred)
val_acc += torch.count_nonzero(pred.eq(title_lab) * (title_lab != 0)).item()
val_total += torch.count_nonzero(title_lab).item()
val_loss /= len(dataloader)
val_acc /= val_total
print(f'Epoch {my_epoch} | Validation Loss: {val_loss:.2f} | Validation Accuracy: {val_acc * 100:.1f}return val_loss, val_acc
epochs = 40
lr = 5e-5
MAX_VOCAB = len(tokenizer)
model = Transformer(num_layers=6, model_dim=256, num_heads=8, dff=2056, vocab_size=MAX_VOCAB).to(device)
print(f'Using {device}')
optimizer = optim.Adam(model.parameters(), lr=lr)
scheduler = CosineWarmupScheduler(optimizer, 5000, MAX_VOCAB * epochs)
criterion = nn.CrossEntropyLoss(ignore_index=0)
train_loss = []
val_loss = []
val_acc = []
model.train()
for epoch in range(1, epochs + 1):
e_loss = train(train_dataloader, model, criterion, optimizer, scheduler, epoch, interval=100)
train_loss += e_loss
v_loss, v_acc = test(test_dataloader, model, criterion, epoch)
val_loss.append(v_loss)
val_acc.append(v_acc)
# Save model
state_dict = model.state_dict()
torch.save(state_dict, "large_model_v2.pt")
# Plot loss and stuff
fig, ax1 = plt.subplots()
ax1.plot(train_loss)
ax1.set_xlabel('Batch num')
ax1.set_ylabel('X-entropy Loss')
ax1.plot(np.arange(1, len(val_loss) + 1) * len(train_dataloader) ,val_loss)
ax1.plot([], [], 'r', label = 'temp') # Just for legends; hack
ax2 = ax1.twinx()
ax2.set_ylabel('Validation Accuracy')
ax2.plot(np.arange(1, len(val_loss) + 1) * len(train_dataloader),
np.array(val_acc) * 100, 'r')
fig.tight_layout()
ax1.legend(['Train loss', 'Test loss', 'Test acc'])
plt.savefig('loss_good.png')
plt.show()
Inference
The above training does take awhile on an A100, and it’s not even the best results. With additional tweaking and modifications, we can probably do a lot better. In addition, we should probably look at a more specific field rather than “astro” as a whole. However, let’s move on to writing the inference.
To build a generator is easy: we start with $(x_0)$ where $x_0$ is the start token and repeatedly query the model conditioned on the abstract input. For example, the first token will be given by $x_0 \to x_1$, which we then pass in $(x_0, x_1) \to (x_1, x_2)$ and iterate. We stop once we encounter a stop token or if it reaches the number of max tokens.
# Reimport so I can load the model in a future date
from transformers import AutoTokenizer
checkpoint = "bert-base-uncased"
tokenizer = AutoTokenizer.from_pretrained(checkpoint)
MAX_VOCAB = len(tokenizer)
model = Transformer(num_layers=6, model_dim=256, num_heads=8, dff=2056, vocab_size=MAX_VOCAB).to(device)
model.load_state_dict(torch.load( "large_model_v2.pt"))
model.eval()
print('Loaded model')
class TitleGenerator(nn.Module):
def __init__(self, transformer_model: nn.Module, my_tokenizer):
super().__init__()
self.model = transformer_model
self.tokenizer = my_tokenizer
def forward(self, x: str):
"""
Given an abstract, it should query the transformer
:param x: Should be the abstract
:return:
"""
# Get tokenized
tokenized = self.tokenizer(x, return_tensors='pt')['input_ids']
tokenized = tokenized.to(device)
output = torch.tensor([[101]]).to(device)
self.model.eval()
with torch.no_grad():
for i in range(128):
probs = self.model(output, tokenized)
pred = probs.argmax(dim=2)
output = torch.cat((output, pred[0, -1].view(1, 1)), dim=1)
if output[0, -1] == 102:
break
return self.tokenizer.decode(output[0])
generate = TitleGenerator(model, tokenizer)
generate('We discuss the combined IRAC/MIPS c2d Spitzer Legacy observations of the Serpens star-forming region. We describe criteria for isolating bona fide YSOs from the extensive background of extragalactic objects.')
generate('We explore the reach of analytical models at one-loop in Perturbation Theory (PT) to accurately describe measurements of the galaxy power spectrum from numerical simulations in redshift space. We consider the validity range in terms of three different diagnostics: 1) the goodness of fit; 2) a figure-of-bias quantifying the error in recovering the fiducial value of a cosmological parameter; 3) an internal consistency check of the theoretical model quantifying the running of the model parameters with the scale cut.')
generate('There has been a discussion for many years on whether the disc in the Milky Way extends down to low metallicity. We aim to address the question by employing a large sample of giant stars with radial velocities and homogeneous metallicities based on the Gaia DR3 XP spectra. We study the 3D velocity distribution of stars in various metallicity ranges, including the very-metal poor regime (VMP, [M/H] <−2.0). We find that a clear disc population starts to emerge only around [M/H] ∼−1.3, and is not visible for [M/H] <−1.6. Using Gaussian Mixture Modeling (GMM), we show that there are two halo populations in the VMP regime: one stationary and one with a net prograde rotation of ∼80km/s. In this low-metallicity range, we are able to place constraints on the contribution of a rotation-supported disc sub-population to a maximum of ∼3%. We compare our results to previous claims of discy VMP stars in both observations and simulations and find that having a prograde halo component could explain most of these. ')
