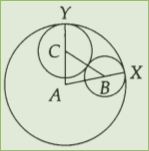
Here’s an excellent question from AoPS:
In the figure to the left, circle $B$ is tangent to circle $A$ at $X$, circle $C$ is tangent to circle $A$ at $Y$, and circles $B$ and $C$ are tangent to each other. If $AB = 6, AC = 5,$ and $BC = 9$, what is $AX$?
The solution really requires no geometry besides the very simple definitions of a circle and a little bit of algebra. Let $r_B, r_C$ be the radius of circles $B, C$ respectively, then we have $r_B + r_C = BC = 9$. Second, $AX = AY = AC + CY = 5 + r_C = 6 + r_B$. Solving these two systems of equation gives 4 and 5. Hence the radius is 10.