Math/Programming – Page 8

March 5, 2014

Is Faster Always Better?

In the Chronicle of Higher Education, there as an article recently discussing early college credits for high-school students. I was surprised that instead of more affluent schools starting these programs, the participants were mostly minorities in already under-achieving schools. This isn’t a way to help bridge the gap between the rich and the poor.

I think one of the key paragraph was the following:

[Studies] have found that students who earn college credits in high school are more likely to continue in college and to graduate on time; some reports have shown a correlation with better grades.

The fact is upper-level college classes are hard. They are hard for the people who are well qualified to be in college, and they are probably near impossible for the others. The unfortunate high school students who took “college class” at their high schools will not be prepared for actual universities. Why is that?

For one, you have much more support in a high school environment in terms of teacher time. Seeing a teacher for 50 minutes a day for a whole week is around an entire lecture worth of more meeting time than my typical 4-credit class. This means that they cover material significantly slower than normal if they follow the same syllabuses as college classes. There won’t be 200 pages worth of reading to do at home per weekend… nor 10 hours problem sets a week (both figures are from my freshman classes).

Next, the hard part of college is the time management. These high school students will not have the same number of distraction as a college student. They’ll never be able to “to turn down the music and pass on parties when they need to study.” Part of this skilled is not just from struggling through freshman and sophomore year either, it comes with maturity in age.

Maybe the most important part is the different atmosphere that college entails. High school was a breeze for me; I never had to spend more than 1 hour on homework typically. Cornell has taught me to trust my classmates and to work together on homework. While the concept of helping others to help yourself (in terms of academics) is incredibly simple, most freshman refuse to do it. They still have a (big) ego to be popped.

So what do I believe should be a good balance between accelerating high school students, and providing cheaper college education?

The classes should be taught at the university, on campus, and by the actual professor. This will ensure that the high school student will receive lecture time equivalent to what he’ll see. I took several FSU classes during my senior year, and I understand the frustration of parking/gas/transportation. Maybe work out some deal to schedule the college class in an appropriate time and bus the students who doesn’t have a car.

Universities should follow the elite colleges and refuse to accept dual enrollment credits unless it can be proven that they’ve learned the material. For me, none of my math classes transferred to Cornell and I am glad it didn’t. It pushed me to take Math 2230 and I gained so much from that class. I know that Caltech and MIT frequently refuse to take AP credits and transfer credits (from high school students), and I believe it’s a good thing. Frequently, students go in to college thinking they’ve mastered the material, until they learned the college likes to focus on an entirely set of different materials.

Most importantly, college classes should only be offered to kids who show promise or are simply ahead of the class. College is hard, and increasingly expensive. Not going to college is probably even more expensive, but it’ll be a disservice to those kids who thought they’ll succeed in college, but ultimately flunk out. I’m not saying one shouldn’t offer advance materials to those failing, but the money which would’ve been going into college credit classes for those only slightly ahead should be going towards hiring better teachers, and creating AP classes.

Article Link or Cornell’s Proxy Link

February 27, 2014

Water

I mentioned that I was 1. making a gif and 2. working on the particle-based fluids for my CS5643 class. Well, here it is.

cube_neigh — With XSPH and tensile instability.

cube_scorr_xsph — Same as above, except different neighbor finding scheme.

February 23, 2014

Life’s Update

I’ve been working on a few things:

Position-based fluids for my CS5643 class, which is a pain to debug. Normally, I have tons of intuition on what numbers are suppose to be but my intuition is nil here. I’m unsure as we’re guessing the correct parameters or even the right formulas and procedure.It’s a great class, just the project are incredibly tedious. For example, my particles right now just seem to float of into the x direction and stay there. Why would it do that?
Hopefully, what ends up happening is something like the following, except less pretty.
I finally installed Hearthstone for my Elementary OS Linux box. It was incredibly easy following this tutorial.
In terms of research, I’ve been reading up on different ways to generate the Krylov basis for GMRES as described in this paper. I’ll probably write up and refined the old “idiot’s guide” again for this paper information (and fix the bad latex in there).
This soundtrack (not allowed to embed).
My card handeling has suffered :(.

February 23, 2014

WISDOM: update

Turns out it just was infected gum.

-_- ugh I hate my life.

February 20, 2014

WISDOM

MY WISDOM TOOTH IS COMING OUT AND IT IS SO ANNOYING. COMBINE THAT WITH CANKER SORES AND A SLIGHT SORE THROAT, MY DAMN MOUTH IS SILLY.

February 20, 2014

Awwducational

Check out that subreddit:

February 11, 2014February 13, 2014

Idiot’s Guide to GMRES (written by and idiot)

I’m doing some programming work for Professor Bindel in the CS department, and it’s pretty novel stuff to me. I figured if I write out what I know about the original method which he is trying to improve on, it’ll help me with the overall picture. Here it is:

The entire premise of GMRES (generalized minimal residual method) is to solve the system of equations like $Ax = b$ where $A$ is a matrices and $x, b$ are vectors with appropriate dimensions. First though, we need some additional machinery before we can cover the main method (don’t worry, the machinery does most of the work).

Overview

First some definitions and an overview before nitty-gritty: a Krylov subspace is a magic thing which is quite simple to think about. It’s defined as $K_k(A, b) = \text{span}\{b, Ab, A^2b, \dots, A^{k-1}b\}$ . It’s really nothing but a series of vectors which we get from multiplying $A$ with $b$ lots of times.

What GMRES aims to do is to minimize the residual ( $A\hat{x} - b$ where $\hat{x} \in K_k(A,b)$ ).

Arnoldi Iterations

I’m going to assume that you seen what the Gram-Schmidt method is; if you don’t recall, it’s the algorithm where given a set of vectors that span a space, you return an orthonormal basis for the subspace which is spans. The Arnoldi iterations are something extremely similar to that, except it’s got a few caveats.

Imagine that we already have a bunch of the vectors from the Krylov subspace from above, but we really can’t work with them. They might be very poorly conditioned in that they’re basically pointing to the same direction (it resembles the power iterations). We basically apply GS on those Krylov vectors to obtain an orthonormal basis. Our end goal is to obtain an expression of the form $AV_{k} = V_{k+1} H_n$ where $A$ was from the matrix defined in our problem and $V$ matrices are the Krylov subspace vectors combined into a matrix. The $H$ is called a upper Hessenberg matrix (i.e. an upper triangular matrix with the first subdiagonal filled in).

The algorithm is as follows (shamelessly copied from wiki):

Start with an arbitrary vector ”q”₁ with norm 1.
Repeat for ”k” = 2, 3, …
$q_k \leftarrow Aq_{k-1} \,$
for j from 1 to k − 1
$h_{j,k-1} \leftarrow q_j^* q_k \,$
$q_k \leftarrow q_k - h_{j,k-1} q_j \,$
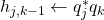
endfor
$h_{k,k-1} \leftarrow \|q_k\| \,$
$q_k \leftarrow \frac{q_k}{h_{k,k-1}} \,$

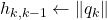
What does it mean? It’s just like (modified) GS! For each additional vector from the Krylov subspace, you take out the stuff that are orthogonal to vectors already processed and store it in the $H$ matrix. Sounds simple but looks rough…

GMRES

Now we can actually get to the method (which is simple if you’re still reading). We try to minimize the residual $\|Ax_n - b\|$ (in the Euclidean norm for those wondering), for $x \in K_k(A, b)$ (i.e. the kth Krylov subspace). We can rewrite that as $x = V_k y$ as from our discussion of the Arnoldi iterations above, $V_k$ is the matrices of the Krylov subspace.

Now, we perform some algebra…

$\|Ax_k - b\|=\|AV_ky - b\|=\|V_{k+1}H_{k+1}y-b\|=\|H_{k+1}y-V_{k+1}^Tb\| + C$

The first equation comes from substitution, the second from using the Arnoldi iterations results, and the last step is kind of tricky. C in our equation is the norm of the projection of b onto the orthogonal complement (i.e. the subspace complement to the space) to the Krylov subspace. Think of this as saying the Pythagorean theorem on the part that lies within the span, and those that lies complement to it.

Finally,
The last bit is just the observation that the first column of $\text{[math]}$ V_{k+1}[\latex] is b, normalized to unit length. So $\text{[math]}$ V_{k+1}^Tb=\|b\|e_1[\latex].

ProblemS with gmres

If you notice the Arnoldi iterations, you have more and more vectors to loop over as the Krylov subspace gets larger… and you have to store all those vectors too! This is why people consistently use GMRES with restarts, where they erase all the previous iterations, and use reconstruct the Krylov subspace from the current, closest solution.

The problem with this, is there are situations where convergence to the solution actually depends on the restart! If you don’t choose a good restart value, convergence to the solution might not occur. That’s bad.

Another way to deal with this is to demand the matrix of vectors by well conditioned… but I don’t know much about this. And another way, is to use Chebychev polynomials to somehow do it (more on this later after I read the paper).

February 10, 2014

The Push

I finally decided to drop algebra, which puts me at 20.5 credit hours this semester. Honestly, it wasn’t a tough decision.

More and more, I see my pure math as an mental excursion to go on when one wants to find fascinating sights. But that’s all it is though, a mental treat as I don’t see myself becoming a pure mathematician.

Am I smart enough for pure math? Maybe.

Am I motivated enough for pure math? Maybe.

One does not pursue grad school when the answer to those questions are just maybe.

January 24, 2014

Perfect Synergy

The past summer, I was at the REU in UMBC. The head of the math department guy preached about the future of mathematics is the intersection of mathematics, statistics and computing; I agree to a large extent.

What I ended up working on seemed to be computing, with more computing, with very little mathematical analysis. The system of differential equations that described pancreatic cells was far too advanced for me to do some significant analysis. Heck, that’s how I feel about most of pure mathematics: the interesting problems are always out of reach from what I know.

Before this past winter break, I found a cool book called “Risk and Reward” in the math library. It’s all about the, surprisingly deep, game of casino blackjack, from the strategies to the mathematics behind the analysis. In the analysis portion of the book, 90

If I ever do become a professor of some sorts, I want to be able to teach a class based on games like blackjack and poker. For projects of sorts, the task will be to calculate the probability of various conditions and to figure out the strategies from the math I provide in class. Maybe for a (optional) final, it’s to actually play the games that we studied in class…

As an exercise over the break, I took an existing program and added the functionality to “practice” the card counting went over the book. It’s based on this project which I butchered (honestly, I spent 2 days doing this… trying to understand someone else’s code is tough). To run the program, make sure Python is installed, and run Blackjack.py. Download

January 17, 2014January 21, 2014

Equation to a Modern Family

On the recent Modern Family episode, Claire was seen giving a lecture to the AP Calculus teacher on how many hours each student are expected to spend each night on school work (totally off for the record…).

Strangely enough there was the word “Schrodinger’s” on the board. Never in AP calculus did I

Do partial differentiation
Learn about Schrodinger’s

To be honest, I’m not entirely sure of the derivation to that equation…

Still, they did get something right! The theorem to the far left seems to be Rolle’s Theorem!