Quirky Quintet

Hopefully this’ll be the first of a many part series to examine CoC in a more mathematical manner, and actually use some of the skills and technologies I have acquired over the years.

The first thing that raiders in CoC know is that time spent not raiding is wasted time. In order to minimize that wasted time, a critical thing to minimize is time spent building troops, spells and resting heroes. Spells and heroes has no build order to minimize, while troops has countless possibilities of building a set army.

The problem is fairly easy to define: given a certain army composition, use the given set of barracks and create that army in the shortest possible time.

Sounds easy right? Meh.

Scheduling Theory

My first impression is to use scheduling theory, and turn it into a simple library call to an approximation algorithm there. Unfortunately, there are several complications.

First of all, since there are multiple barracks, this is a multiple processor problem. Multiple processor problem are actually NP-hard, equivalent to the partitioning problem. Many heuristics exist for a standard problem of many processor, and many jobs for minimizing time. The standard is longest processing time first (LPT).

If one simply implements LPT on this problem, we have a weird problem. The heuristic was designed for processors of equal power, and barracks of different levels have different capacity. The second (more minor problem) is that we need to impose the constraint that a barrack can produce that particular troop (i.e. level 1 creating a P.E.K.K.A).

So in essence, this problem became much tougher using this approach. I guess I can read up on heterogenous processor research, but that’s for another day.

Integer programming

The next approach was to convert it to an integer programming problem.

Let us define our problem then. Let 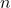be the number of barracks, and 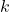be the number of different types of troops (defined to be 10 by the current patch, but let’s keep it flexible). Let 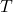be a column matrix of time to produce a single barbarian, archer etc., and 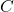be a column matrix of the corresponding capacity needed to train a troop. This means that both 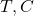have height 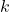. We define a matrix 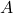such that each entry 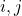corresponds to the 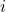th barracks and 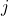th type of troop (by barracks level). For example, the position at (2, 3) corresponds to the 2nd barracks and Giants.

We simply want to minimize the maximal entry of the matrix 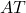such that 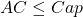where 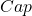is the capacity of each barrack with regards to level.

The unfortunate thing about this whole section is that there is no known general way to solve integer programing problems in polynomial time; it is also NP-hard. Many heuristics are available, and many sub-cases solved, but I’m not at that level yet. One technique which I suspect might do well is to simply relax the problem to a linear programming problem, and then round the result. Thing is, this LP relaxation method kind of sucks most of the time.

Conclusion

So do I have a final product? Nope.

Scheduling theory proves to have little Python implementations, while integer programming is only available from obscure libraries. The best thing to do might be to create my own little meta-heuristic.